Pengenalan Algoritma EM
Algoritma EM merupakan sebuah metode optimisasi iteratif untuk estimasi Maksimum Likelihood (ML) yang berguna dalam permasalahan data yang tidak lengkap (incomplete data). Dalam setiap iterasi pada Algoritma EM ini terdapat 2 tahap, yaitu tahap Ekspektasi atau tahap E (E step) dan tahap Maksimisasi atau tahap M (M step). Algoritma EM ini hampir mirip dengan pendekatan ad hoc untuk proses estimasi dengan missing data yaitu (1) mengganti missing value dengan estimated value, (2) mengestimasi parameter, (3) mengestimasi ulang missing value tadi dengan menggunakan parameter baru yang diestimasi, (4) mengestimasi ulang parameter, dan seterusnya berulang-ulang sampai dengan konvergen terhadap suatu nilai.
Ide dasar dari Algoritma EM ini adalah mengasosiasikan suatu complete data problem dengan incomplete data problem dengan tujuan agar secara komputasi menjadi lebih mudah.
E step dan M step
E step bertujuan menemukan ekspektasi bersyarat dari missing data dengan syarat data yang diketahui nilainya (observed) dan penduga parameternya, kemudian mensubstitusikan nilai ekspektasi yang diperoleh terhadap missing data. Dalam hal ini missing data yang dimaksud bukanlah Ymiss tapi fungsi dari Ymiss yang muncul dalam complete data loglikelihood, yaitu ℓ(θ ∣ Y).
Misal θ(t) adalah penduga parameter θ saat ini dan misal Ymiss = Z, maka E step pada EM bermaksud mencari ekspektasi loglikelihoodnya jika θ adalah θ(t):
𝒬(θ∣θ(t)) = E(Ymiss∣ Y;θ(t)) [ℓ (θ;Y)]
= ∫ ℓ(θ;Y) f(Ymiss∣Yobs,θ = θ(t)) 𝒹Ymiss (pers. 1)
Kemudian, M step pada EM menentukan θ(t+1) dengan memaksimumkan ekspektasi loglikelihood tersebut.
𝒬(θ(t+1) ∣ θ(t)) ≥ 𝒬(θ ∣ θ(t)) , untuk semua θ
 (pers. 2)
(pers. 2)
Atau secara ringkas algoritma EM diberikan sebagai berikut:
-
E-step : estimasi statistik cukup (sufficient statistic) untuk data lengkap Yt dengan cara menghitung nilai ekspektasinya.
-
M-step: Tentukan
 dengan metode MLE (Maximum Likelihood Estimation) dari Yt
dengan metode MLE (Maximum Likelihood Estimation) dari Yt -
Iterasi sampai nilai θ(t) konvergen, atau θ(t+1) – θ(t) mendekati nol. Hasilnya adalah sequence dari nilai-nilai θ(0) -> θ(1) -> … dimulai dari suatu nilai θ(0) tertentu. Secara umum, iterative algoritma adalah aturan yang applicable untuk nilai θ(0) tertentu.
Kelebihan dan kekurangan Algoritma EM
Algoritma EM memiliki sifat yang lebih baik di banding pendekatan atau metode lainnya. Beberapa keunggulan Algoritma EM dibanding pendekatan lainnya yaitu antara lain:
1. Algoritma EM lebih stabil secara numerik, dimana dalam setiap iterasinya loglikelihood-nya naik.
2. Dibawah kondisi umum, algoritma EM konvergen terhadap suatu nilai reliabel. Yaitu dengan dimulai suatu nilai sembarang θ(0) akan hampir selalu konvergen terhadap suatu lokal maximizer, terkecuali salah dalam mengambil nilai awal θ(0).
3. Algoritma EM cenderung mudah diterapkan, karena bersandarkan pada penghitungan complete data.
4. Algoritma EM mudah diprogram, karena tidak melibatkan baik integral ataupun turunan dari likelihood.
5. Algoritma EM hanya memakan sedikit ruang harddisk dan memori di komputer karena tidak menggunakan matriks ataupun invers-nya dalam setiap iterasi.
6. Analisis lebih mudah dibanding metode lain.
7. Dengan memperhatikan kenaikan monoton likelihood pada iterasi, maka mudah untuk memonitor konvergensi dan kesalahan program.
8. Bisa digunakan untuk mengestimasi nilai dari missing data.
Adapun kelemahan dari Algoritma EM antara lai n:
1. Tidak menyediakan prosedur untuk menghasilkan estimasi matriks kovarian dari penduga parameter.
2. Algoritma EM bisa saja konvergen secara lambat, yaitu jika terlalu banyak incomplete information.
3.Algoritma EM tidak menjamin akan konvergen pada suatu nilai maksimum global jika terdapat multipel maksima.
4. Dalam beberapa masalah, E step mungkin secara analisis akan degil (intractable).
Contoh
Kasus Multinomial (Contoh dari paper Dempster)
Terdapat data pengamatan dari 197 hewan yang terdistribusi secara multinomial ke dalam empat kategori, dimana:
y = (y1, y2, y3, y4) =(125, 18, 20, 34)
dengan peluang masing-masing sel (½+¼π, ¼(1-π), ¼(1-π), ¼π)
memiliki fungsi distribusi peluang:
 (pers. 3)
(pers. 3)
Misal y merupakan incomplete data dari suatu populasi multinomial dengan lima kategori x= (x1, x2, x3, x4, x5) dimana y1=x1+x2, y2=x3, y3=x4, y4=x5, dengan fungsi distribusi:
 (pers. 4)
(pers. 4)
Untuk mendefinisikan Algoritma EM, akan ditunjukkan bagaimana mencari π(p+1) dari π(p), dimana π(p) adalah nilai π setelah iterasi ke-p, untuk p=0,1,2,… . Seperti dinyatakan diatas, Algoritma EM terdiri dari 2 langkah:
-
E step mengestimasi sufficient statistics dari complete data
x, dengan syarat data teramati y. Dalam contoh ini (x3, x4, x5) diketahui, sehingga sufficient statistics yang harus diestimasi hanya untuk x1 dan x2, dimana x1+x2= y1=125. Sehingga x1 dan x2 bisa diestimasi menggunakan suatu nilai π. Dalam hal ini perlu inisiasi dari π. (pers. 5)
(pers. 5) -
M step kemudian menggunakan hasil estimasi complete data (x1(p), x2(p), x3, x4, x5) untuk mengestimasi π menggunakan maksimum likelihood dengan memperlakukan hasil estimasi complete data sebagai data pengamatan, yang kemudian akan menghasilkan:
 (pers. 6)
(pers. 6)Algoritma EM dalam contoh ini yaitu dengan melakukan berulang-ulang langkah diatas.
Dimulai dengan nilai awal π=0.500, algoritma bergerak untuk 8 langkah seperti terlihat pada tabel 1. Kolom kedua pada tabel 1 menunjukkan selisih antara π(p) dengan π*, sedangkan kolom ketiga menunjukkan rasio selisih pada kolom 2 terhadap iterasi sebelumnya.
Nilai π* diperoleh dengan mensubstitusikan x2(p) dari persamaan 5 kedalam persamaan 6, dan memisalkan π*= π(p)= π(p+1) maka akan terbentuk suatu persamaan kuadratik untuk MLE dari π dengan solusi:
π* = (15+√(53809))/394 =~ 0,6268214980
Tabel 1

Berikut ini adalah macro Minitab untuk contoh diatas:
gmacro
Contoh1
Note oO0 Minitab Macro untuk Contoh EM Algorithm, Dempster paper 0Oo
Note
Note “Masukkan Tingkat Akurasi Deviasi Parameter”
Erase c1-c5 c100-c105
Set c100;
file ‘terminal’;
Nobs 1.
Note “Masukkan Nilai Awal pi Yang Diinginkan”
Set c101;
file ‘terminal’;
Nobs 1.
Let k100=c100(1)
Let k101=c101(1)
Let k1=125 #y1
Let k2=18 #y2
Let k3=20 #y3
Let k4=34 #y4
Let k5=(15+sqrt(53809))/394 #penduga pi
Let k102=k101 # pi p
Let k103=k5-k102 # selisih pi p thdp pi *
Let k104=1
Name c1 ‘x1’
Name c2 ‘x2’
Name c3 ‘pi’
Name c4 ‘pi-pi*’
Name c5 ‘Rasio’
While k103>k100
Let k6=k1*(0.5/(0.5+0.25*k102)) #x1p
Let k7=k1*((0.25*k102)/(0.5+0.25*k102)) #x2p
Let c1(k104)=k6
Let c2(k104)=k7
Let c3(k104)=k102
Let c4(k104)=k103
Let k102=(k7+k4)/(k7+k4+k2+k3)
Let k103=k5-k102
If k104>1
Let k106=c4(k104)/c4(k104-1)
Let c5(k104-1)=k106
Endif
Let k104=k104+1
Endwhile
Endmacro
Kasus Univariat Normal
Misal yi iid (identicaly independent distibution) berdistribusi N(μ,σ2) dimana yi untuk i=1, …, m teramati, yi untuk i=m+1, …, n missing dan diasumsikan missing secara acak atau missing at random (MAR). Maka ekspektasi dari setiap yi dengan syarat Yobs dan θ = (μ, σ2) adalah μ.
Fungsi distribusi bersama dari yi adalah:
 (pers. 7)
(pers. 7)Maka fungsi loglikelihood diberikan oleh:
 (pers. 8)
(pers. 8)Dan diperoleh sufficient statistik Σyi dan Σ yi2. Kemudian dengan E step dalam algoritma EM dihitung:
 (pers. 9)
(pers. 9)untuk penduga parameter θ(t)= (μ, σ(t)). Tanpa ada missing data, MLE dari parameter μ adalah (Σyi)/n dan untuk σ2 adalah ((Σyi2)/n)-((Σyi)/n)2.
Lalu M step menghitung:
 (pers. 10)
(pers. 10)Pasang μ(t) = μ(t+1) = μ̂ dan σ(t) = σ(t+1) = σ̂ dan ulangi langkah pada E step. Akan terlihat bahwa iterasi ini akan konvergen pada:

dan
 (pers. 11)
(pers. 11)yang merupakan MLE dari μ dan σ2 dari Yobs dengan mengasumsikan data missing at random (MAR). Contoh ini hanya untuk menggambarkan langkah-langkah dalam algoritma EM, tentu saja EM sebenarnya tidak diperlukan untuk contoh soal ini. Karena pada contoh ini MLE-nya dapat mudah diketahui. Algoritma EM bermanfaat bila MLE parameter sulit diketahui.
Berikut adalah macro Minitab untuk simulasi contoh diatas:
gmacro
Contoh2
Note oO0 Minitab Macro untuk Contoh EM Algorithm, Dempster paper 0Oo
Note Simulasi Data Observasi Pada Kolom C1
Note
call Simulasi1
Note “Masukkan Tingkat Akurasi Deviasi Parameter”
Note
Set c100;
file ‘terminal’;
Nobs 1.
Note “Masukkan Nilai Awal Mu Yang Diinginkan”
Set c101;
file ‘terminal’;
Nobs 1.
Note “Masukkan Nilai Varian Yang Diinginkan”
Set c102;
file ‘terminal’;
NObs 1.
copy c1 c99.
erase c1
let k98=count(c99)
Let k100=c100(1)
Let k101=c101(1) #Mu awal
Let k102=c102(1) #Varian awal
Let k103=k105 #n-m
Let k1=sum(c99) #sum of yi
Let c97=c99**2
Let k2=sum(c97) #sum square of yi
Let k3=k1/k98 #penduga Mu
Let k4=abs(k3-k101) # selisih Mu p thdp Mu *
Name c1 ‘Mean’
Name c2 ‘Varian’
Name c3 ‘Selisih Mean’
Let k104=1
While k4>k100
Let k6=k1+k103*k101
Let k7=k2+(k103*(k101**2+k102))
Let c1(k104)=k101
Let c2(k104)=k102
Let c3(k104)=k4
Let k101=k6/(k103+k98)
Let k102=(k7/(k103+k98))-(k101**2)
Let k4=abs(k3-k101)
Let k104=k104+1
Endwhile
Endmacro
#
#
gmacro
Simulasi1
Note >>Macro untuk membuat simulasi Data Observasi<<
Note dengan Missing Data
Note
erase c1-c15 c90-c110
Note Masukkan jumlah data observasi:
Set c100;
file ‘terminal’;
Nobs 1.
Note Masukkan jumlah missing Data:
Set c101;
file ‘terminal’;
Nobs 1.
Let k1=c100(1)
Let k105=c101(1)
Rand k1 c1;
Normal 4 2.
Rand k105 c99;
Integer 3 k1.
Do k4=1:k105
let k5=c99(k4)
let c1(k5)=miss()
enddo
endmacro
Kasus Bivariate Normal
Misal W=(W1, W2)T adalah vektor random bivariate yang berdistribusi Normal
W ~ N(μ, Σ)
dengan vektor rata-rata μ=(μ1, μ2)T dan matriks kovarian:

Fungsi distribusi peluang dari bivariate normal diberikan oleh:
 pers. 12
pers. 12dengan vektor parameter ψ diberikan oleh:

Andaikan kita akan mencari MLE dari ψ pada sampel random berukuran n dari populasi W, dimana data ke-i variate Wi
missing sejumlah mi unit (i= 1,2). Misal data kita beri label wj = (w1j, w2j)T dengan j = 1, 2, 3, …, m menyatakan data yang teramati, dimana m = n – m1 – m2, w2j (j=m+1, m+2, …, m+m1) menyatakan m1 data pengamatan dengan missing data pada variate pertama w1j. Dan w1j (j= m+m1+1, …, n) menyatakan m2 pengamatan dimana terdapat missing data pada variate kedua w2j.Dengan menggunakan log-likelihood akan diperoleh suatu sufficient statistics (statistik cukup) untuk μi dan σ2ij berikut:
T = (T1, T2, T11, T12, T22) , dimana:
 pers. 13
pers. 13Dan MLE untuk bivariate normal adalah:
 pers. 14
pers. 14Dari sifat distribusi bivariat normal yang diketahui, distribusi bersyarat dari W2 syarat W1=w1 adalah berdistribusi normal dengan mean:
 pers.15
pers.15dan varians
 pers. 16
pers. 16Selanjutnya,
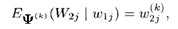 dimana:
dimana: pers. 17
pers. 17dan
 pers. 18
pers. 18untuk j=m+m1+1, …, n. Dengan cara yang sama Eψ(k)(W1j ∣ w2j) dan Eψ(k)(W1j2∣ w2j) bisa diperoleh dengan cara mengganti subskrip 2 menjadi 1 dan sebaliknya pada persamaan 17 dan 18.

assalamu alaikum, bapak saya ingin bertanya mengenai EM. sebelumnya terima kasih karena sudah share tentang EM. TA saya berhubungan dengan EM pada rancangan percobaan RAK(two way classiofication). dengan missing value yg ada cukup banya. apakah bisa dibantu untuk oftware yang digunakan atau cara perhitungannya? terima kasih sebelumnya
pak saya mau tanya. TA saya membahas algoritma em pada kasus distribusi multivariat normal. biasanya software yg digunakan untuk kasus ini apa ya pak? makasih bapak sebelumnya sudah berbagi ilmu.
salam kenal,
Pak, apakah punya contoh aplikasi logaritma EM dalam PROC IML/SAS?
Thanks.
salam kenal pak..
saya james.. skg saya sedang mengerjakan ta berkaitan dengan algoritma em untuk segmentation di image processing microarray.. apa bapak pny sran source buku ato website yang ada tutorial atau alat bantu begtu pak..
trima kasih sebelumnya..
salam kenal juga… maaf baru balas. Hmmm kalo bahan pustaka tentang EM yang advanced (khususnya di bidang Anda) saya juga belum tau. Kalo basicnya ya dari buku The EM Algorithm and Extention. Kalo untuk programming-nya sepertinya di MATLAB banyak toolbox untuk image processing.
ass. saya reni dan skrg lagi ngerjakan skripsi dengan judul estimasi model laird ware berdasarkan estimator MLE (maximum likelihood estimate) dan BLP(best linear prediction) dengan menggunakan algoritma em. yg saya tanyakan algoritma EM yg saya gunakan agak berbeda. mohon penjelasannya
bisa saja beda.. EM alg yang saya tulis untuk estimasi missing data, namun intinya ya tetap E-step dan M-step. Mungkin penjelasannya bisa Anda dapatkan di buku The EM Algorithm and Extention.
iya pakk..
saya tuggu 🙂
trimakasih..
Dag nabbit good stuff you whpsnerppaipers!
Alt du tar blir til gull – sÃ¥nn er det bare! Nydelig alt sammen. Du er virkelig en sann inspirasjonskilde Marie, og jeg gleder meg til hver gang jeg titter innom her for det er alltid noe nytt og spennende. Takk!! Ha en superfin helg 🙂 Klem
bapak, saya citra,
saya sedang mengerjakan skripsi tentang algoritma EM..
boleh minta tolong kalau misalnya contohnya adalah regresi linier berganda..
terimakasih..
Wah maaf ternyata komennya masuk spam.. insya Allah saya usahakan nanti saya hub lewat email saja ya
aslkm pak sya hnif…
trimaskih sblumnya mau shre EM..kbtlan sy mo TA mslah anlis EM,,,tlong mita cntoh ksus pak,,?yg lbh lngkap…
@hanif: selain artikel sebelumnya, smoga artikel yang baru saya posting disini bisa membantu memberi inspirasi 😀